2025年全国高中数学联合竞赛B卷一试

这份试卷细致考察了高中数学诸多学科的关键内容与技巧，对学生整体能力期待很高。

一、代数板块

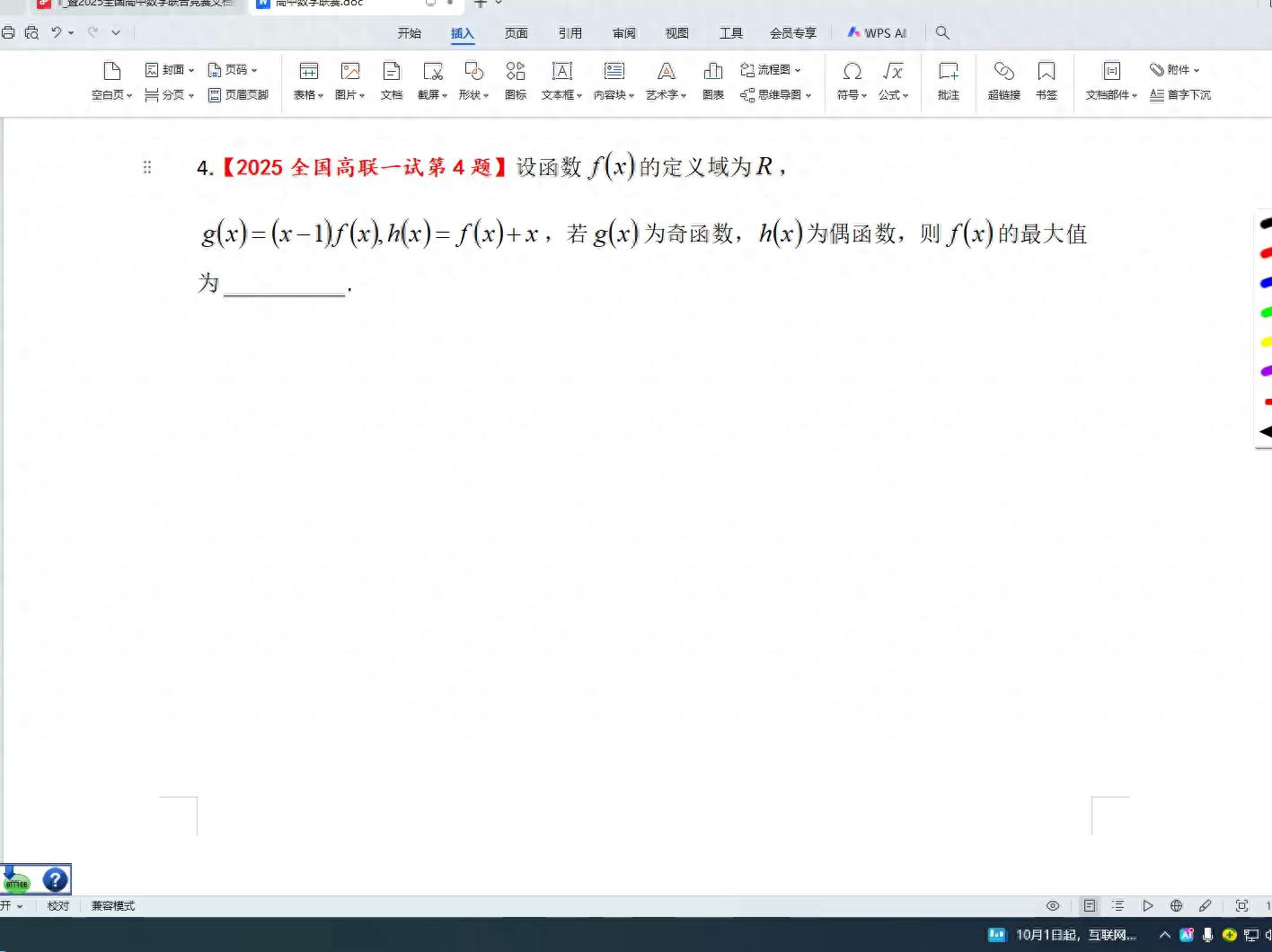
代数在试卷中占比较大，考察内容包含函数、数列、不等式、复数和向量等。函数部分，将方程、对数、指数结合起来考察其性质和运算，例如借助对数换底公式以及等比数列特性来解对数方程，这既需要熟练掌握对数运算，又要求理解等比数列的特点。数列部分，主要涉及基本数列的性质和运算方法。不等式部分，重点在于基本不等式的运用，需要通过灵活变换代数式来匹配公式。多项式考察虚数部分、实数部分的定义和计算方法，以及长度的求解，通过判断复数为实数的情形来设定变量并计算长度，每一步都紧密相连。向量则与长度和点积相关联，借助单向量特性及三角不等式来寻找最大值或最小值。这一部分的关键点在于多种知识的整合，例如在复杂情形下精确使用对数和数列的相关内容来解决问题，代数式的转换对思维敏捷度和计算能力提出了很高标准，诸如基础不等式的变换处理、复数和向量运算中条件的运用，均需学生具备牢固的基本功和敏锐的观察能力。

二、几何板块

涉及平面几何和解析几何,平面几何没有单独的大题,但是一些填空题考察了三角形和圆的特性,例如通过正弦定理和椭圆焦点三角形内角正切值来计算椭圆离心率,需要从几何关联转向代数计算。解析几何涉及椭圆和直线的知识，例如求椭圆的离心率，以及直线与曲线交点的问题，需要学生熟悉椭圆的基本特性，掌握直线方程，并具备良好的计算和逻辑思维能力，比如通过联立方程求交点坐标和有关量的取值范围，这类计算过程复杂且容易产生错误，对学生耐心和细致的要求很高。

三、概率与统计板块

这份试卷借助组合数学考察概率，比如从 20 个数字里挑选 4 个数字，让它们的乘积成为 2025 的倍数，必须先拆解 2025 的构成要素，再根据不同情况设计选取方案，最后应用组合数学方法进行求解，这对学生区分情况讨论和推理判断能力有很高标准，怎样做到各类情况既不重复也不遗漏，正是解题的核心所在，也是最大的挑战。

四、其他板块

集合和整数平方数等少数内容被提及，例如指数幂与集合的关联，测试集合处理和整数特性，期望学生能准确把握整数相关定义，并从集合信息中识别数论规律。试卷考察点覆盖广泛，强调知识融会贯通和思维能力的评估，对学生知识积累、解题方法、计算水平及心理状态都有严格标准。